GSDS Home

Introduction

What's new in WellSim

FAQ

What is WellSim ?

Tutorials

Getting familiar with WellSim

Entering well geometry

Entering well data

Discharge simulations

Improving a discharge simulation

Output simulations

Tips for using WellSim

Changing how WellSim looks

Reservoir drawdown simulation

Injection simulations

Injectivity simulations

Advanced simulations

Reference

How WellSim works

Managing databases

Graphs

Exporting data

Importing data

Units

Preferences

References

Glossary

Installing WellSim

For evaluation

Setup with a key

On another PC

Upgrading WellSim

Registration

Single-user dongle

Network dongle

Uninstalling

Tutorial: Injectivity simulations

An injectivity simulation calculates wellhead pressures at different steady-state mass flowrates for a well injection. The result is called an injectivity curve; usually this is used to predict predict the pump pressure required to inject at a given mass flowrate. For more on injectivity simulations see here.

• An injectivity simulation can be TopDown, BottomUp or TestData (TestData is usually best) read more. The tutorial describes a TestData and a TopDown simulation.

• The tutorial uses:

  • the measured injectivity curve Test rate data - 1 that you should have entered earlier.

  • the injection simulation Td 110 barg 860 t/hr that you should have entered earlier.

• Measure all depths relative to the same point at the wellhead read more. Ensure Finish depth is the depth of the deepest feedzone.

• Entering and running an injectivity simulation is similar to an output simulation. If you are unsure what to do here, review output simulations.

Pumped or free-flowing wells

This tutorial covers pumped injection wells, where for all mass flowrates the fluid has to be pumped into the well, the wellhead pressure is positive and the fluid is liquid throughout the well. Note that a pumped well can become free-flowing at low mass flowrates; you can see this in the injectivity simulation by the wellhead pressure becoming close to zero.

Free-flowing wells can (perhaps only at low mass flowrates) accept fluid without pumping and have a wellhead pressure close to zero, see this tutorial.

Running a TestData injectivity simulation

This TestData injectivity simulation uses the measured injectivity curve Test rate data - 1. Assume CO2 is 5,000 ppm and NaCl is 0 ppm (both in total fluid) at the deepest feedzone.

1. In the sample database, open a new injectivity simulation for .

2. Enter these values:

   

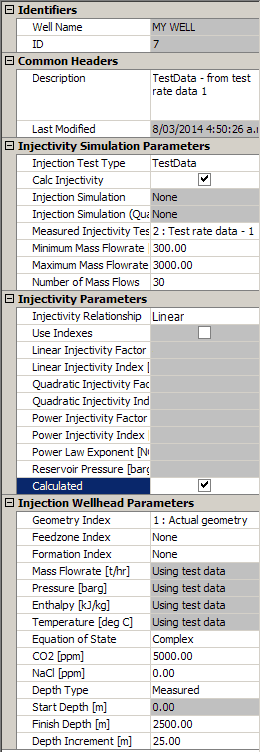
   Note:

   • Select an Injection test type of TestData, then load the measured injectivity curve from the Measured Injectivity Test dropdown list. You can then click the Injection Test Rates tab to see the measured injectivity curve data.

   • Ensure there is a tick under Reservoir pressure so WellSim will calculate this.

3. Preprocess, run and save the new simulation:

   • WellSim calculates the linear injectivity factor (0.115 barg/t/hr) and the reservoir pressure (207.53 barg).

   • To stop the run, click .

   • If you get the error Solution did not converge see here.

Interpreting an injectivity simulation

1. Go to measured injectivity curves, tag Test rate data - 1, click Graph, click Apply to 2nd worksheet.

2. Go to injectivity simulations, tag TestData - from test rate data - 1.

3. Click MultipleGraph. If necessary, change the graph to:

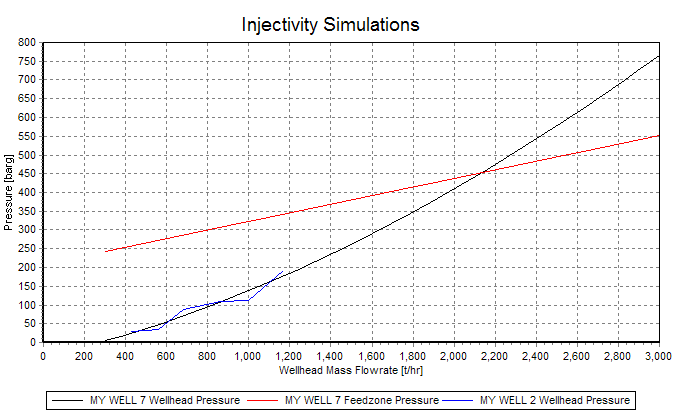
Red line: Pressure at the deepest feedzone:

• This is linear because we chose a Linear injectivity simulation.
• The slope is the linear injectivity factor calculated by the injectivity simulation (0.115 barg/t/hr).
• At zero mass flowrate, the series would pass through 207.5 barg, the reservoir pressure calculated by the injectivity simulation.

Black line: Pressure at the wellhead.

• At low massflowrates, friction is negligible and the pressure (vertical distance) between the pressure at the deepest feedzone and the wellhead is the static pressure of water 2.5 km deep, about 250 barg.

• At higher mass flowrates, friction rises and dominates static water pressure at the right side of the graph, where the pressure series rises well above the pressure at the deepest feedzone. Even though the injectivity simulation is Linear, the pressure at the wellhead is not linear, but quadratic.

Blue line: The measured injection curve, Test rate data - 1, used for the injectivity simulation.

• The injectivity simulation has extrapolated these points to higher pressures. You can see the measurement errors in the measured curve.

Running a TopDown injectivity simulation

This uses the TopDown injection simulation Td 110 barg 860 t/hr. Also, assume reservoir pressure is 207 barg (the value calculated by the above injectivity simulation), CO2 is 5,000 ppm and NaCl is 0 ppm (in total fluid) as above.

1. In the sample database, open a new injectivity simulation for .

2. Enter these values:

   

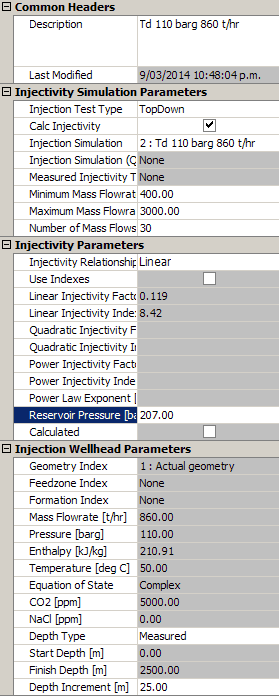
3. Preprocess, run and save the new simulation.

Note

1. WellSim calculates the linear injectivity factor, 0.119 bar/t/hr. This is very close to 0.118 bar/t/hr, which is the 'actual' value calculated by the output simulation From better TD 100 t/hr see here.

2. This is surprising, because the data used for the injection simulation Td 110 barg 860 t/hr is probably not very accurate.

3. What has happened is that the reservoir pressure we assumed above (207 barg) is also in error compared to the 'actual' value of 200 barg used in the output simulation From better TD 100 t/hr. And the two errors have cancelled each other out.

4. If you rerun the above injectivity simulation and enter a reservoir pressure of 200 barg then it calculates the linear injectivity factor to be 0.127 bar/t/hr, suitably in error.